最大実体公差方式
- 最大実体公差方式とは
- 一般事項
- 用語
- 穴に対する位置度公差
- データム平面に関連する穴の直角度公差
- データム平面に関連する軸の直角度公差
- 軸線の真直度公差
- データム平面に関連する軸の平行度公差
- ゼロ幾何公差方式
最大実体公差方式とは
機械製図の中で最も難しい概念のひとつが最大実体公差方式だと思います。理解してしまえばすごく便利で必要なものだと考えることができますが、理解するまではやっかいな存在かもしれません。
最大実体公差方式の必要性を簡単に説明すると、はまり合うように設計されている2種類の部品が、実際にはめ合わせてみると”はまらない”ということが起きないようにすることと、はめ合わせるために過剰に厳しい寸法公差を設定するのを防ぐためのものです。
1つの穴と軸に対してのはめ合わせの場合は、はめあい方式によるはめあい公差を適用すれば問題ありません(幾何公差が必要な場合を除く)。しかし、下記のような2つ以上の穴と軸では、個別のはめあい公差を満たしていても位置がズレていればはまり合わないこともあります。
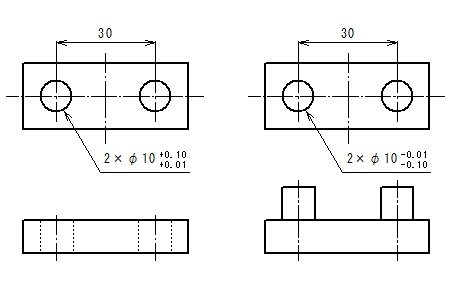
※ここでは説明のため、省略されている寸法は理論値、幾何公差は0となっているものとします。また、分かりやすいように、はめあい公差の記号は使用せずキリの良い数値を使用しています。
設計する人は、この2つの部品の穴と軸の各寸法が最悪の状態でもはまり合うように設計しなければなりません。最悪の状態とは軸径が最大(φ9.99)で、穴径が最小(φ10.01)の状態です。その差は0.02となり、2つの部品の位置寸法である30寸法の差も0.02以内に抑えなければならないので、30寸法に公差をつけるならば、30±0.01となります。
もし、30±0.02にしてしまうと、一方の部品が29.98で、もう一方の部品が30.02の場合に、差が0.04になってしまうのではめ合わせることができません。
しかし、軸径が最小(φ9.90)で、穴径が最大(φ10.10)の場合は、30±0.1でもはめ合わせることはできるので、この寸法公差は過剰に厳しいと言わざるを得ません。過剰に厳しい公差は加工コストを増大させてしまいます。
このような場合に最大実体公差方式を適用します。幾何公差の数値は、軸径と穴径が最悪の状態でもはめ合わせることが出来る最大の数値を記入します。
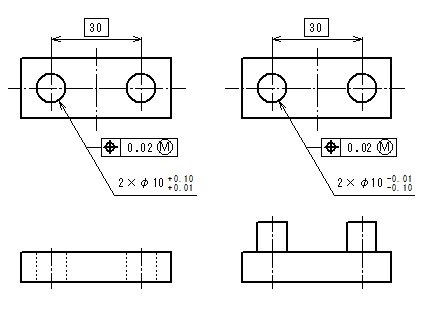
このとき許容される位置度公差は、2つの穴径が同じ、または2つの軸径が同じ場合、下記の表のようになります。
| 穴径 | 許容される位置度公差 |
|---|---|
| φ10.01 | 0.02 |
| φ10.04 | 0.05 |
| φ10.07 | 0.08 |
| φ10.1 | 0.11 |
| 軸径 | 許容される位置度公差 |
|---|---|
| φ9.9 | 0.11 |
| φ9.93 | 0.08 |
| φ9.96 | 0.05 |
| φ9.99 | 0.02 |
一般に、許容される幾何公差の計算式は下記のようになります。
許容される幾何公差=指示された幾何公差の値 + |最大実体寸法 - 実際の寸法|※"| |"内は絶対値
一般事項
- 最大実体公差方式は、公差付き形体に対する実効状態を越えないことを要求する公差方式である。
- データムに対して指示される場合には、データム形体に対する完全形状の最大実体状態を越えないことを要求する。
- この公差方式を適用する場合には、記号を指示する。
- この公差方式は、軸線または中心平面に適用し、寸法と幾何公差との間の相互依存関係を考慮している。
- 公差付き形体に適用する場合には、対象とする公差付き形体が許容限界寸法内でその最大実体状態から離れていると、形体が実効状態を越えないという条件で、指示した幾何公差を増加させることができる。
- データム形体に適用する場合には、データム軸直線または中心平面は、データム形体が許容限界寸法内で最大実体状態から離れていると、公差付き形体に関連して浮動してもよく、浮動の値は最大実体寸法とデータム形体のはまり合う寸法との差に等しい。
最大実体公差方式での用語
- 局部実寸法…形体の任意の断面における個々の距離、すなわち、任意の相対する2点間で測定した寸法
- 最大実体状態…形体のどこにおいても、その形体の実体が最大となるような許容限界寸法。例えば、最小の穴径、最大の軸径を持つ形体の状態。
- 最大実体寸法…形体の最大実体状態を決める寸法。
- 最小実体状態…形体のどこにおいても、その形体の実体が最小となるような許容限界寸法。例えば、最大の穴径、最小の軸径をもつ形体の状態。
- 最小実体寸法…形体の最小実体状態を決める寸法。
- 実効状態…図面指示によってその形体に許容される完全形状の限界であり、この状態は、最大実体寸法と幾何公差との総合効果によって生じる。
- 実効寸法…形体の実効状態を決める寸法。
穴に対する位置度公差
- 穴の直径が最大実体状態、つまり穴径が最小の状態では、位置度公差は指示された値となる。
- 穴の直径が最小実体状態、つまり穴径が最大の状態では、位置度公差は指示された値に、最大の穴径と最小の穴径の差をプラスした値となる。
- 許容される位置度公差 = 指示された位置度公差 + (実際の穴径 - 最小の穴径)
対応するピンが最も好ましくない状態のもとでも、部品の組付けが可能な穴となる。
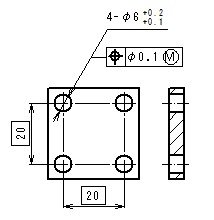
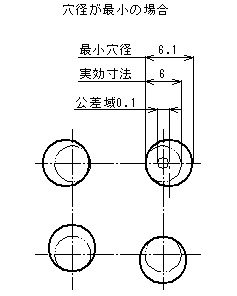
指示例と説明
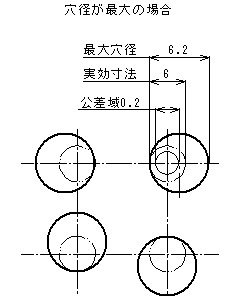
- 形体の個々の局部実寸法は、φ6.1とφ6.2の間になければならない。
- すべての公差付き形体は、それぞれが他の穴に対して、理論的に正確な位置にある場合に、φ6(=φ6.1-φ0.1)の完全形状の内接円筒の境界外になければならない。
- したがって、形体の軸線は、形体のそれぞれの直径がφ6.1の最大実体寸法であるときには、φ0.1の位置度公差の公差内に、形体のそれぞれの直径がφ6.2の最小実体寸法であるときには、φ0.2までの位置度公差の公差内で変動してもよい。
データム平面に関連する穴の直角度公差
- 穴の直径が最大実体状態、つまり穴径が最小の状態では、直角度公差は指示された値となる。
- 穴の直径が最小実体状態、つまり穴径が最大の状態では、直角度公差は指示された値に、最大の穴径と最小の穴径の差をプラスした値となる。
- 許容される直角度公差 = 指示された直角度公差 + (実際の穴径 - 最小の穴径)
対応するピンが最も好ましくない状態のもとでも、部品の組付けが可能な穴となる。
指示例と説明
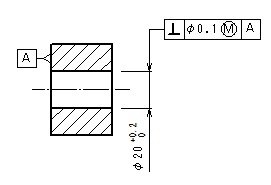
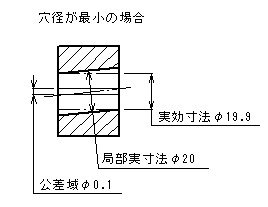
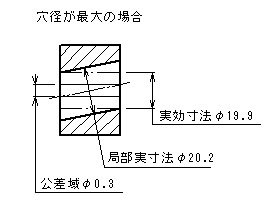
- 形体の個々の局部実寸法は、φ20とφ20.2の間になければならない。
- 公差付き形体は、実効状態の境界外、すなわちデータム平面Aに直角で、φ19.9(=φ20-φ0.1)の完全形状の内接円筒外になければならない。
- したがって、形体のすべての直径がφ20の最大実体寸法であるときには、直角度公差はφ0.1、形体のすべての直径がφ20.2の最小実体寸法であるときには、直角度公差φ0.3までの公差内で変動してもよい。
データム平面に関連する軸の直角度公差
- 軸の直径が最大実体状態、つまり軸径が最大の状態では、直角度公差は指示された値となる。
- 軸の直径が最小実体状態、つまり軸径が最小の状態では、直角度公差は指示された値に、最大の軸径と最小の軸径の差をプラスした値となる。
- 許容される直角度公差 = 指示された直角度公差 + (最大の軸径 - 実際の軸径)
対応する穴が最も好ましくない状態のもとでも、部品の組付けが可能な軸となる。
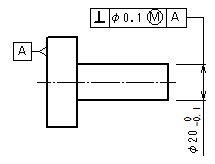
指示例と説明
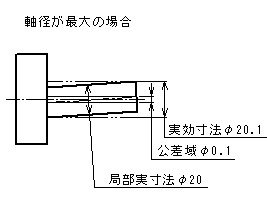
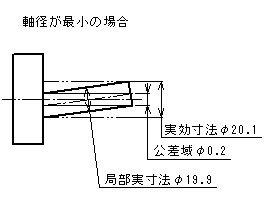
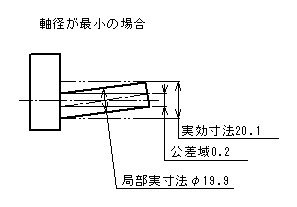
- 形体の個々の局部実寸法は、φ19.9とφ20の間になければならない。
- 公差付き形体は、実効状態φ20.1(=φ20+φ0.1)を越えてはならない。
- したがって、形体のすべての直径がφ20の最大実体寸法であるときには、直角度公差はφ0.1、形体のすべての直径がφ19.9の最小実体寸法であるときには、直角度公差φ0.2までの公差内で変動してもよい。
軸線の真直度公差
- 軸の直径が最大実体状態、つまり軸径が最大の状態では、真直度公差は指示された値となる。
- 軸の直径が最小実体状態、つまり軸径が最小の状態では、真直度公差は指示された値に、最大の軸径と最小の軸径の差をプラスした値となる。
- 許容される真直度公差 = 指示された真直度公差 + (最大の軸径 - 実際の軸径)
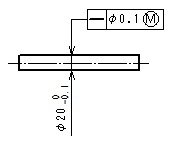
指示例と説明
- 形体の個々の局部実寸法は、φ19.9とφ20の間になければならない。
- 公差付き形体は、実効状態φ20.1(=φ20+φ0.1)を越えてはならない。
- したがって、形体のすべての直径がφ20の最大実体寸法であるときには、真直度公差はφ0.1、形体のすべての直径がφ19.9の最小実体寸法であるときには、真直度公差φ0.2までの公差内で変動してもよい。
データム平面に関連する軸の平行度公差
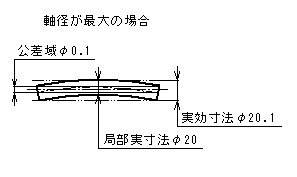
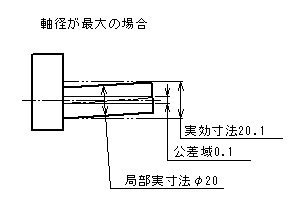
- 軸の直径が最大実体状態、つまり軸径が最大の状態では、平行度公差は指示された値となる。
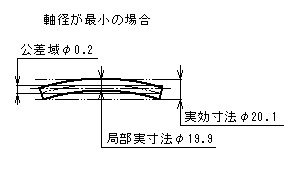
- 軸の直径が最小実体状態、つまり軸径が最小の状態では、平行度公差は指示された値に、最大の軸径と最小の軸径の差をプラスした値となる。
- 許容される平行度公差 = 指示された平行度公差 + (最大の軸径 - 実際の軸径)
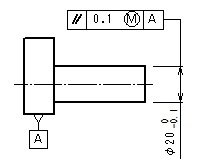
指示例と説明
- 形体の個々の局部実寸法は、φ19.9とφ20の間になければならない。
- 公差付き形体は、データム平面Aに平行で20.1(=20+0.1)離れた平行二平面の実効状態内になければならない。
- したがって、形体のすべての直径がφ20の最大実体寸法であるときには、平行度公差は0.1、形体のすべての直径がφ19.9の最小実体寸法であるときには、平行度公差0.2までの公差内で変動してもよい。
ゼロ幾何公差方式
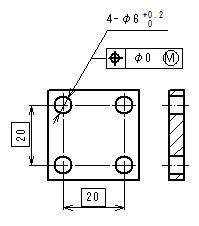
- 形体の個々の局部実寸法は、φ6とφ6.2の間になければならない。
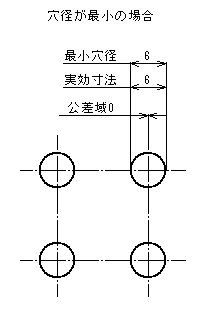
- すべての公差付き形体は、それぞれが他の穴に対して、理論的に正確な位置にある場合に、φ6(=φ6-φ0)の完全形状の内接円筒の境界外になければならない。
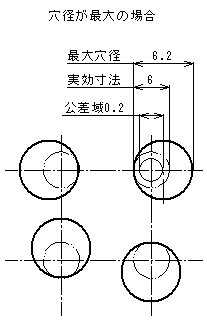
- したがって、形体の軸線は、形体のそれぞれの直径がφ6の最大実体寸法であるときには、φ0の位置度公差となり、形体のそれぞれの直径がφ6.2の最小実体寸法であるときには、φ0.2までの位置度公差の公差内で変動してもよい。
- JIS B 0023:1996 製図-幾何公差表示方式-最大実体公差方式及び最小実体公差方式